Multiplication des nombres décimaux

Vos élèves ont des problèmes pour multiplier des nombres décimaux?

Au calcul 1,52 x 10, ils répondent 1,520 ?

Ils vous disent, à juste titre, qu'ils ont appris  qu'on "ajoute" un zéro à un nombre multiplié par 10.

Nous "bidouillons"  alors en expliquant que cette règle ne vaut que pour les nombres entiers et pas pour les nombres décimaux, ce qu'ils ont du mal à comprendre; ce qui est normal vu que ce n'est pas logique. Et surtout c'est mathématiquement erroné.

J'ai eu l'occasion de lire il y a quelques années, une méthode très simple qui marche très bien. J'avais effectué  quelques lectures pédagogiques dans le cadre de ma préparation à un stage de SRAN (remise à niveau) d'un groupe d'élèves d'une autre école qui avait de grosses difficultés dans ce domaine.

En 15 min le problème était résolu durablement.

Cette "méthode" consiste à expliquer l'origine de l'"ajout" du zéro. En CE2, pour la multiplication des nombres entiers, on peut ensuite continuer à effectuer le raccourci très connu "on écrit un zéro à la fin d'un nombre multiplié par 10, deux 0 à un nombre multiplié par 100, etc....."

En CM, il suffira de rappeler l'explication de base et de la systématiser pour les multiplications des nombres décimaux.

Car pour multiplier un nombre entier ou un nombre décimal par 10, on emploie le même système, le même mécanisme.

L'explication peut se résumer ainsi: le décalage des nombres.

Le plus simple pour commencer consiste à repartir du tableau de numération.

Multiplier un nombre par 10 consiste à décaler un nombre (qui par défaut se termine toujours dans la case des unités) de la case des unités à la case des dizaines (10: case des dizaines). Donc un décalage d'une case vers la gauche.

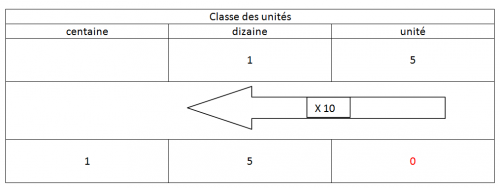
Quand je multiplie 15 par 10 , j'inscris 15 dans mon tableau de numération et je fais le geste de tirer, de décaler le nombre d'une case (vers la gauche).  La case des unités se retrouve alors "vide". Je la comble par un zéro (pour la petite histoire, le zéro n'est pas "ajouté", il est déjà présent car 15 c'est pareil que 15,000. Quand je multiplie  15 par 10 et que je décale  vers la gauche d'une case mon chiffre 15,000 je me retrouve  avec 150,00, précision utile pour les CM quand vous aurez à expliquer le résultat d'1,5 x 100 par exemple).

Pour les nombres décimaux, c'est pareil. 

Attention ce n'est pas la virgule qui bouge mais c'est le nombre qui se décale.

La virgule marquera toujours la limite entre les nombres entiers et les nombres décimaux.

Dans votre tableau de numération, le nombre se décale du nombre de cases demandées, la virgule ne bouge pas.

Il suffit de faire un geste de tirer vers la gauche votre nombre dans le tableau et généralement même pas besoin de passer par les tableaux individuels à tirettes.

Très rapidement ensuite, plus besoin de tableau de numération, le geste est dans la tête et on peut décaler sans problème.

Pour 1,52 x10, je décale d'une case mon nombre vers la gauche (sans bouger de place ma virgule) et hop j'obtiens 15,2.

3,54 x10, je tire d'une case et hop 35,4.

5,652 x10, je tire et hop 56,52......... 

NB: Avec les élèves, vous pouvez fabriquer des tableaux de numération à tirettes où vous pouvez décaler les nombres en fonction de la multiplication (d'une case quand vous multipliez par 10, de 2 cases quand vous multipliez par 100, etc.....).

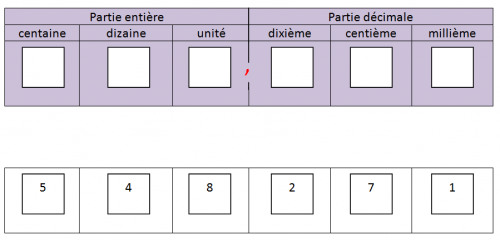
Dans la partie violette, évider les cases blanches et faire passer des bandelettes de chiffres. Placer un nombre et le décaler selon la multiplication par 10, par 100,....

La bandelette de chiffres doit pouvoir se manipuler facilement (en mettant un système de languette de chaque côté, par exemple).

Chez Val10 et Pascale vous trouverez des ressources sur ce sujet.

Pour diviser des nombres décimaux par 10 c'est le même principe sauf qu'au lieu de "tirer" d'une case vers la gauche vous "poussez" d'une case vers la droite.

15,24 x 10 =  152,4

15,24 / 10 = 1,524

Pour diviser par 100 vous "poussez" de 2 cases vers la droite, pour diviser par 1000 vous "poussez" de 3 cases vers la droite, etc...

Télécharger « Le tableau de numération avec les décimaux.pdf »